6.2.2 Point Spread Function

The combined effects of the aberrations introduced in the wavefront by the instrumentation and by environmental effects such as, for ground-based observations, the atmospheric turbulence, are conveniently described in terms of the global Point Spread Function (PSF) $P(\mathbf{d})$, giving the probability density that a photon will hit the imaging device at a point that is displaced by a vector $\mathbf{d}$ from where it would have hit it in the absence of aberrations. If the true surface brightness distribution of an object is $\Sigma_t(\mathbf{r})$, then the observed surface brightness distribution will be

$$\Sigma_{obs}(\mathbf{r})= \int \,P(\mathbf{r-r'})\,\Sigma_{t}(\mathbf{r'})\,\mathrm{d}^2\mathbf{r'}= \left[P\otimes\Sigma_{t}\right](\mathbf{r})$$ (6.1)

where $\otimes$ indicates the convolution operator. This latter notation is convenient e.g. when simulating the blurring of a ``true'' image due to a given PSF, as it will be done in the simulation of GAIA observations in Section 6.3, since one can then exploit the fact that the Fourier transform of the convolution of two functions equals the product of the Fourier transforms of the two functions. Roughly speaking, the ``width'' of the PSF, characterized e.g. by its FWHM or by the diameter enclosing a given percentage of the total brighness, thus describes the angular resolution achieved in an observation.

As mentioned in Subsection 3.2.3, in ground-based observations obtained with telescopes of moderately large apertures, the PSF is dominated by the phenomenon of seeing, described in 1.1. Conversely, in space observations the PSF is essentially due to instrumental aberrations only, and the careful polishing of the telescope optics may therefore in principle yield nearly diffraction-limited images. This is almost the case for HST WFPC2, where however the image undersampling due to the large pixel area on the sky have sensible effects, but not for GAIA, where the continuous scanning of the satellite and the adopted CCD binning strategy substantially widens the purely optical PSF.

The PSF of HST WFPC2 is accurately described by [Holtzman et al. 1995a] and [Biretta et al. 1996]. In particular, it is therein shown that when observations with the broad-band, $UBVRI$-like WFPC2 filters are made, the 50%-light diameter, i.e. the diameter of the circle enclosing 50% of the light coming from a point-like source, is about 80 and 130 mas for the PC and the WFCs respectively.

The PSF of GAIA BBP, which will be needed in the simulation of observations, was modelled and numerically calculated under realistic assumptions about the instrumental performance following [Lindegren 1998a]. An adaptation of a program by Lennart Lindegren written by Anthony Brown was used to calculate the PSF and output it as a fits file.

As a first step, the monochromatic optical PSF is derived, taking into account the diffraction from the telescope rectangular aperture and the aberrations of the wavefront introduced by the optical defects of the mirrors. For the latter, the Matra Marconi Space baseline assumption of primary and tertiary mirrors polished to $\lambda/30~\textrm{rms}$ and secondary mirror polished to $\lambda/50~\textrm{rms}$ was used. Then the monochromatic global PSF is derived by considering the pixel and sample binning, the efficiency of the charge transfer and of the Time Delay Integration, and finally the across-scan motion of the image during the scan. Here, the four sample sizes of $6\times8$, $6\times4$, $6\times2$ and $1\times8$ pixels were separately considered. Finally, the polychromatic global PSF, or PSF proper, is computed by adding up the contributions to the PSF due to light of different wavelengths, taking into account the true spectrum of the source, the telescope transmittance and the CCD response curve. Thus, the PSF for any stellar spectral type can be obtained. For our purposes, as explained in Section 5.4, the spectrum of a G2V star can be chosen as representative of the spectrum of a typical galaxy. The PSF thus obtained is also referred to as the one-scan PSF, indicating that it is the true PSF of each GAIA BBP observation. In order to model the all-mission effective PSF, i.e. the PSF of an image obtained from superposition of many observations, a set of 50 randomly distributed scan directions was generated, the one-scan PSF was accordingly rotated using bilinear interpolation and the rotated PSFs were finally summed. The result of this procedure is believed to reliably represent the all-mission effective PSF, provided that an efficient stacking strategy is devised.

The properties of the resulting PSFs are illustrated in Figures 6.2 and 6.3, showing the one-scan and 50-scan PSFs for the four sample sizes, respectively. The first plot of each row is a a contour plot of the two-dimensional PSF, with the brightest contour drawn at a surface brightness level 0.5 mag fainter than the maximum and altogether seven contours drawn at intervals of one magnitude. In the second one, the encircled energy curve of the PSF is given, whereas in the third and fourth ones the one-dimensional PSF profiles in the along-scan and across-scan direction are drawn.

Figure 6.2: GAIA one-scan PSFs. From the top: (a) $6\times8$ pixels/sample, (b) $6\times4$, (c) $6\times2$, (d) $1\times8$. See text for details.

Figure 6.3: GAIA 50-scan PSFs. From the top: (a) $6\times8$ pixels/sample, (b) $6\times4$, (c) $6\times2$, (d) $1\times8$. See text for details.

Several features are easily noted in these two Figures. Generally speaking, the width of the PSFs is dominated by the sample size, and even the one-scan PSF obtained with the square sample of $6\times2$ pixels appears almost perfectly circular, notwithstanding the elliptical Airy Disk delivered by the telescope optics. It also appears that, owing to wave-front errors, the one-scan PSFs are not exactly centered at the point (0,0), and that the 50-scan PSFs show significant deviations from a circular shape, mostly due to random fluctuations in the scan directions. Besides, in general the encircled energy curve does not appear to depend on the number of scans.

The 50%-light diameter $d_{50}$ and the 90%-light diameter $d_{90}$ (i.e. the diameters of the circles enclosing 50% and 90% of the energy, respectively) of the 50-scan PSFs are given by Table 6.2 together with the FWHM, the latter given by the average of the FWHMs along the two directions.

Table 6.2: Values of $d_{50}$, $d_{90}$ and FWHM for GAIA all-mission PSFs. 50%-light diameter, 90%-light diameter and FWHM of GAIA 50-scan PSFs for different sample sizes.

	$d_{50}$	$d_{90}$	FWHM
$6\times8$	520	940	400
$6\times4$	340	640	345
$6\times2$	270	560	255
$1\times8$	480	900	145

It should be noted that $d_{50}$ and $d_{90}$ depend significantly on the length of the sample major side but not much on the sample minor side, suggesting to use a nearly square sample to optimize the observations with respect to angular resolution. It also appears that $d_{50}$ and the FWHM can be very different, $d_{50}$ usually being larger than the FWHM, and it can be observed that the difference increases with the PSF asymmetry, which in turn increases with the $y/x$ ratio of the sample size. The PSF obtained with $1\times8$ pixels/sample has e.g. a much smaller FWHM but not a substantially smaller $d_{50}$ if compared with that obtained with $6\times8$ pixels/sample. This was to be expected, since an asymmetric PSF has relatively wider wings. However, this effect is not particularly significant for the two smaller and more symmetric sample sizes of $6\times4$ and $6\times2$ pixels.

The all-mission effective PSF obtained from simulations will most likely be slightly wider than given above, since the HST and GAIA PSFs both contribute to smear the true sky. Taking this into account, the 50%-light diameter can be estimated by means of the quadratic formula

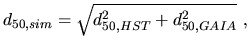$$d_{50,sim}=\sqrt{d_{50,HST}^2+d_{50,GAIA}^2}~,$$ (6.2)

which however gives values that do not differ much from those given in Table 6.2 for any combination of WFPC2 camera and BBP sample size.