


Next: 2.2 The Spacecraft
Up: 2. The GAIA Mission
Previous: 2. The GAIA Mission
Contents
2.1 The Measurement Principle and the Scanning Law
The main objective of the GAIA mission is to perform global or wide field
astrometry as opposed to local or narrow field astrometry. In local
astrometry a star's position can only be measured with respect to
neighbouring stars in the same field. Even with an accurate instrument,
the errors become prohibitive when making a survey, due to the need
of combining measurements obtained in different fields, and thus affected
by systematic and accidental errors. The principle of global astrometry, is
instead to link stars with large angular distances in a network where each
star is connected to a large number of other stars in every direction.
In order to do so, the measurement of large angular distances through
the simultaneous observation of two fields of view separated by a large angle
is required.
This principle, first demonstrated by the success of the Hipparcos mission,
can be exemplified by the problems encountered in the measurement of stellar
parallaxes as it can be obtained with narrow-field instruments, illustrated
in Figure 2.1.
These are usually based on the measurement of the motion of a star S with
respect to a number of background stars near to S on the sky, which are
themselves in parallactic motion.
The relation between the relative parallax
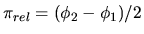 of S with respect to a generic background star S
of S with respect to a generic background star S and the absolute parallax
of S
and the absolute parallax
of S  is then
is then
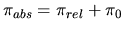 , where
, where 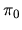 is the
absolute parallax of S
is the
absolute parallax of S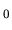 .
In practice, one has to estimate the average absolute parallax of the
background stars, and this estimation introduces an error that usually
dominates the global error budget.
This limitation presently does not allow to measure parallaxes with an
accuracy better than about a few mas.
In wide-field astrometry, instead, the measurement of large angular distances
allows one to measure the absolute parallax
.
In practice, one has to estimate the average absolute parallax of the
background stars, and this estimation introduces an error that usually
dominates the global error budget.
This limitation presently does not allow to measure parallaxes with an
accuracy better than about a few mas.
In wide-field astrometry, instead, the measurement of large angular distances
allows one to measure the absolute parallax
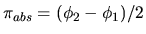 of a
star without the need to apply poorly determined correction factors, and the
accuracy can thus be improved by orders of magnitude.
of a
star without the need to apply poorly determined correction factors, and the
accuracy can thus be improved by orders of magnitude.
Figure 2.1:
Narrow-field and wide-field astrometry. In narrow-field astrometry
the measurement of the parallax of a star S involves the application of a
poorly determined correction to the observed value to take into account the
parallactic motion of background stars such as S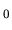 , whereas in wide-field
astrometry one can directly measure absolute parallaxes, thus obtaining a much
better accuracy.
, whereas in wide-field
astrometry one can directly measure absolute parallaxes, thus obtaining a much
better accuracy.
|
|
Accordingly, the GAIA payload must therefore provide two lines of sight, which
can be obtained either with a single telescope and a beam combiner, as in
Hipparcos, or with two separate telescopes.
In either case, an high stability and an accurate knowledge of the variations
of the basic angle between the two lines of sight is required in order to
calibrate the astrometric measurements.
The beam combiner option, however, leads to severe opto-mechanical
problems for large-aperture (say above one meter or so) telescopes.
Besides, the superposition of two fields of view onto a single focal plane
causes crowding and object confusion on the focal plane, which become
appreciable when observing faint objects. Therefore, the two-telescope
concept was retained for the GAIA design and later refined with the
inclusion of a third spectrometric telescope.
Figure 2.2:
GAIA scanning law. The satellite spin and Sun axes at an angle of 55
deg are indicated, together with the lines of sight of the two
astrometric instruments and two consecutive great circles.
The satellite spin period is of about 3 hours, and the corresponding
scanning speed is thus of 120 arcsec/s.
|
|
For a continuous accurate calibration of the basic angle, the two astrometric
lines of sight must point to the same sky regions at small time intervals.
This is achieved by means of an axisymmetric payload and a three-hour period
(i.e. 120 arcsec/s) spin motion of the satellite about its symmetry
axis, which is perpendicular to the instruments' lines of sight. From the
instruments' standpoint, the stars thus cross each field of view with a
uniform motion. As for Hipparcos, the scan direction is a privileged one,
and the position measurements are essentially performed in this direction
only.
The complete and uniform sky coverage that is needed to build the star
network is then obtained through a slow precession of the spin axis about
the Sun axis. The angle between these two axes, or Sun angle, is thus kept
constant, in order to minimize the thermal gradients in the payload.
For GAIA, the optimization of the scanning law has led to a un angle
of 55 deg (43 deg for Hipparcos) and a precession period of 72 days
(57 days for Hipparcos). This scanning law ensures that each sky region
is observed several times during the whole mission with
nearly isotropic orientations of the scanning directions.
The slow precession of the spin axis generates a line of sight motion
across scan of 0.51 deg over a spin period, while the field of
view height is 0.68 deg. The overlapping between consecutive scans
allows the calibration of some instrumental parameters such as the basic
angle using the same stars.
The GAIA scanning law is illustrated in Figure 2.2, while
its typical sky coverage pattern is exemplified by the actual scanning of
the Hipparcos satellite over a short period shown in
Figure 2.3.
Figure 2.3:
GAIA/Hipparcos sky coverage.
The top figure shows the path of Hipparcos spin axis over a four-month
period. The scan direction is indicated by the arrows. The bottom figure
shows the actual scanning by Hipparcos during one complete precession
of the spin axis (57 days). For clarity, only one reference great circle
out of five is indicated. The actual scanning is five times denser.
|
|
The apparent peculiarity of the adopted observation strategy
draws a sharp distinction between scanning satellites like GAIA
and conventional ``point-and-stare'' space observatories such as
the HST. The distinction is fairly similar to the one existing
between conventional ground-based telescopes and meridian circles,
i.e. the telescopes that are typically used for ground-based
astrometric measurements. Like meridian circles, GAIA will only
detect relatively bright stars, due to the short exposure times that are
allowed by a continuously scanning instrument.
Unlike meridian circles, however, GAIA will be able to combine
many observations of any sky region, obtained at different epochs
and at different position angles, so as to significantly raise the
all-mission signal-to-noise ratio.
The number of observations of a given sky region mainly depends on
its ecliptic latitude, owing to the fact that the chosen scanning
pattern is symmetrical with respect to the Sun-satellite direction.
The number of observations of 5000 random sky regions by both astrometric
instruments is given as a function of the ecliptic latitude for a
5-year mission in Figure 2.4. The maximum, average and minimum
number of observations are about 420, 170 and 100 (i.e. 210, 85 and 50 per
astrometric instrument), respectively, where the latter value is obtained for
sky regions near the ecliptic.
Figure 2.4:
Number of observations of 5000 random sky regions by both astrometric
instruments over a 5-year mission as function of ecliptic latitude.
The average number of observations is 170.
Courtesy of Lennart Lindegren, Lund Observatory.
|
|



Next: 2.2 The Spacecraft
Up: 2. The GAIA Mission
Previous: 2. The GAIA Mission
Contents
Mattia Vaccari
2000-12-05
![]() of S with respect to a generic background star S
of S with respect to a generic background star S![]() and the absolute parallax
of S
and the absolute parallax
of S ![]() is then
is then
![]() , where
, where ![]() is the
absolute parallax of S
is the
absolute parallax of S![]() .
In practice, one has to estimate the average absolute parallax of the
background stars, and this estimation introduces an error that usually
dominates the global error budget.
This limitation presently does not allow to measure parallaxes with an
accuracy better than about a few mas.
In wide-field astrometry, instead, the measurement of large angular distances
allows one to measure the absolute parallax
.
In practice, one has to estimate the average absolute parallax of the
background stars, and this estimation introduces an error that usually
dominates the global error budget.
This limitation presently does not allow to measure parallaxes with an
accuracy better than about a few mas.
In wide-field astrometry, instead, the measurement of large angular distances
allows one to measure the absolute parallax
![]() of a
star without the need to apply poorly determined correction factors, and the
accuracy can thus be improved by orders of magnitude.
of a
star without the need to apply poorly determined correction factors, and the
accuracy can thus be improved by orders of magnitude.
![\includegraphics[width=\textwidth]{./figures/glo_ast.eps}](img53.gif)
![\includegraphics*[width=0.55\textwidth]{./figures/scanlaw.ps}](img54.gif)
![\includegraphics[width=0.55\textwidth]{./figures/hipp_fig013.eps}](img55.gif)
![\includegraphics*[width=0.7\textwidth]{./figures/numofscans.ps}](img56.gif)