


Next: 4.5 Model's Validity and
Up: 4.4 Surface Brightness Distribution
Previous: 4.4.1 Elliptical Galaxies
Contents
4.4.2 Disk Galaxies
As first suggested by [de Vaucouleurs 1959], the surface brightness radial profile of
disk galaxies can be interpreted as the sum of two components, the so called
bulge component following the 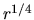 law and the so called disk component
following the exponential law
law and the so called disk component
following the exponential law
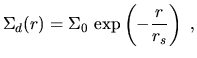 |
(4.9) |
where 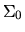 is the central surface brightness and
is the central surface brightness and 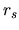 is the so called
disk scale length. Equation 4.9 can be rewritten in a form similar
to the one used for the
is the so called
disk scale length. Equation 4.9 can be rewritten in a form similar
to the one used for the 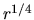 law as
law as
![$\displaystyle \Sigma_d(r)=\Sigma_e\,\exp\left[-1.6783\left(\frac{r}{r_e}-1\right)\right]$](img207.gif) |
(4.10) |
where
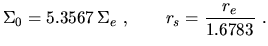 |
(4.11) |
Since the first systematic study of [Freeman 1970], this law has been
known to fit the profiles of the outer regions of a large class of disk
galaxies and has, in fact, come to define the typical surface brightness
profile of the intrinsically flat component of disk galaxies, to the extent
that deviations from these profile are generally ascribed to the existence
of other components or to the effects of dust.
Assuming this analytical form for the profile of the disk component, one can
then try to disentangle the contributions of the bulge and disk components
by means of fitting techniques.
The methods for doing this have in time undergone a great development, from
the simple one-dimensional fitting procedure along the galaxy major axis first
adopted by [Freeman 1970] to the bidimensional decomposition techniques
currently being developed, which are applied to whole galaxy images
(see e.g. [Byun and Freeman 1995]).
In this study, a bulge+disk profile will be considered, combining an 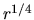 law with an exponential law, thus not considering contributions from components
such as spiral arms, bars, rings, lenses, or the photometric effcts of dust.
The most general form of such a profile
law with an exponential law, thus not considering contributions from components
such as spiral arms, bars, rings, lenses, or the photometric effcts of dust.
The most general form of such a profile
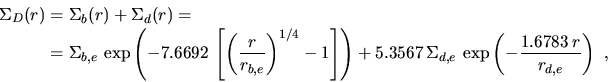 |
(4.12) |
depends on two pairs of parameters characterizing the bulge and disk
components, respectively.
The only independent variable we have so far introduced in our model is the
total magnitude, which however determines also the effective radius through
Equation 4.3.
Therefore, the values of two other parameters must be given in order
to completely determine the form of Equation 4.12.
A convenient choice are two quantities derived from bulge/disk decompositions
and frequently reported in the literature, namely the bulge/bulge+disk ratio
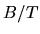 , or the ratio between the brightness contributed by the bulge component
and the total brightness, and the ratio
, or the ratio between the brightness contributed by the bulge component
and the total brightness, and the ratio
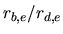 between the
effective radii of the bulge and disk components. As shown in
Appendix D, these two parameters completely determine the
bulge+disk profile.
As for
between the
effective radii of the bulge and disk components. As shown in
Appendix D, these two parameters completely determine the
bulge+disk profile.
As for 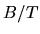 , [Kent 1985] found that in intrinsically luminous D galaxies
this is tightly correlated with the morphological type, falling from a mean
value of 0.65 for S0 to a mean value of 0.15 for Sc and later types.
Recently, [Ratnatunga et al. 1999] found a mean
, [Kent 1985] found that in intrinsically luminous D galaxies
this is tightly correlated with the morphological type, falling from a mean
value of 0.65 for S0 to a mean value of 0.15 for Sc and later types.
Recently, [Ratnatunga et al. 1999] found a mean 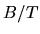 of 0.4 from the bulge/disk
decomposition of the MDS galaxies. The same two references then agree in
fixing to about 0.5 the mean value of
of 0.4 from the bulge/disk
decomposition of the MDS galaxies. The same two references then agree in
fixing to about 0.5 the mean value of
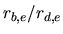 .
Such an excellent agreement between parameters obtained from galaxies of
largely different magnitudes suggested to consider the two parameters as
fixed, without introducing in the model the complications of other free
parameters. Values of
.
Such an excellent agreement between parameters obtained from galaxies of
largely different magnitudes suggested to consider the two parameters as
fixed, without introducing in the model the complications of other free
parameters. Values of 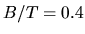 , corresponding to a bulge/disk ratio
, corresponding to a bulge/disk ratio
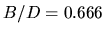 , and
, and
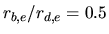 were therefore assumed.
With our choices for
were therefore assumed.
With our choices for 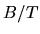 and
and
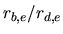 the bulge+disk profile
becomes
the bulge+disk profile
becomes
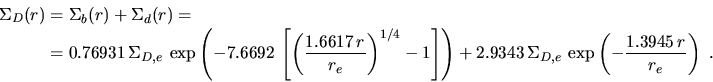 |
(4.13) |
In general, the bulge and disk components dominate the profile at small
and large radii, respectively. Note, however, that due to the analytical
form of the two profiles, at very large radii the bulge contribution
eventually exceeds that of the disk. In fact, practically all (99%) of the
brightness predicted by the disk profile falls within 4 effective radii,
but for the bulge profile only 85% of the light is within 4 effective radii,
and the model needs to extend out to about 19 effective radii to contain 99%
of it.
Shifting to a magnitude scale, the analytical expression for 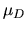 is not
as simple as that derived for ellipticals and is
is not
as simple as that derived for ellipticals and is
![$\displaystyle \mu_D(r)=\mu_{D,e}-2.5\,\log\left[ 0.76931\,\exp\left(-7.6692\,\l...
...1/4}-1\right]\right)+2.9343\,\exp \left(-\frac{1.3945\,r}{r_e} \right)\right]~.$](img217.gif) |
(4.14) |
The total brightness emitted by the galaxy and the effective surface
brightness can be written as
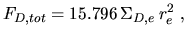 |
(4.15) |
and
![$\displaystyle \mu_{D,e}=2.5\,\log(15.796)+5\,\log(r_{e,\mathrm{[as]}})+I_{\mathrm{[mag]}} ~~~\mathrm{[number~deg^{-2}~mag^{-1}]}~.$](img219.gif) |
(4.16) |
Table 4.5 reports the values of
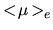 ,
, 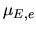 and
and
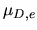 for different total
for different total 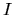 magnitudes.
The values therein listed in the second column will be used in
Chapter 5 to estimate the number of galaxies that could be
detected by GAIA ASM.
On the other hand, the values listed in the third and fourth column will be
used to estimate the standard error of GAIA broad-band photometry at the
effective radius of a galaxy.
magnitudes.
The values therein listed in the second column will be used in
Chapter 5 to estimate the number of galaxies that could be
detected by GAIA ASM.
On the other hand, the values listed in the third and fourth column will be
used to estimate the standard error of GAIA broad-band photometry at the
effective radius of a galaxy.



Next: 4.5 Model's Validity and
Up: 4.4 Surface Brightness Distribution
Previous: 4.4.1 Elliptical Galaxies
Contents
Mattia Vaccari
2000-12-05
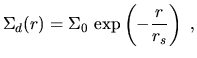
![$\displaystyle \Sigma_d(r)=\Sigma_e\,\exp\left[-1.6783\left(\frac{r}{r_e}-1\right)\right]$](img207.gif)