


Next: 4.3 Angular Size
Up: 4. Statistical Model of
Previous: 4.1 Morphological Classification
Contents
4.2 Number Counts
Galaxy differential number counts, giving the number of galaxies per unit sky
area per unit magnitude interval as function of total magnitude, have always
been a classical tool of observational cosmology.
Consequently, a great effort has always been devoted to the extension of the
observations to deeper magnitudes, larger sky regions and a wider range of
colors.
In particular, in the past few years 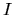 -band counts at high Galactic
latitudes have been reliably extended down to
-band counts at high Galactic
latitudes have been reliably extended down to
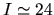 , as summarized
e.g. by [Shimasaku and Fukugita 1998]. In our model, counts from three different sources
were combined in order to cover as large a magnitude range as possible.
At bright magnitudes, i.e. for
, as summarized
e.g. by [Shimasaku and Fukugita 1998]. In our model, counts from three different sources
were combined in order to cover as large a magnitude range as possible.
At bright magnitudes, i.e. for 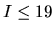 , well-established counts were
provided by [Lattanzi 1997], whereas at fainter magnitudes results from
[Glazebrook et al. 1995] (
, well-established counts were
provided by [Lattanzi 1997], whereas at fainter magnitudes results from
[Glazebrook et al. 1995] (
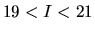 ) and [Abraham et al. 1996b] (
) and [Abraham et al. 1996b] (
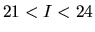 )
were used. A least-square polynomial fit in
)
were used. A least-square polynomial fit in 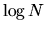 vs.
vs. 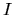 was
performed on these data, in order to assess the consistency of the three
sources and to obtain a functional form
was
performed on these data, in order to assess the consistency of the three
sources and to obtain a functional form 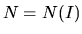 for use in the following.
It was thus found that a second degree polynomial was sufficient to obtain
a good fit to the data.
The number counts and the best-fit parabola are shown in
Figure 4.2, while the best-fit parameters are given
in Table 4.2.
According to this approximation, the differential number counts take the
following functional form
for use in the following.
It was thus found that a second degree polynomial was sufficient to obtain
a good fit to the data.
The number counts and the best-fit parabola are shown in
Figure 4.2, while the best-fit parameters are given
in Table 4.2.
According to this approximation, the differential number counts take the
following functional form
![$\displaystyle N(I)=\textrm{dex}\,(a_N+b_N\,I+c_N\,I^2)~~~\mathrm{[number~deg^{-2}~mag^{-1}]}~,$](img158.gif) |
(4.1) |
where ``dex'' stands for the exponential function in base ten.
Values of the three parameters contained in Equation 4.1 are given
in Table 4.2, while counts calculated with this formula are given
in Table 4.4.
The cumulative galaxy number counts, giving the total number of galaxies per
unit sky area brighter than a given 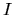 magnitude
magnitude 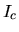 , are then given by
the definite integral
, are then given by
the definite integral
![$\displaystyle N_c(I) = \int_{-\infty}^{I} N \,\mathrm{d}I'~~~\mathrm{[number~deg^{-2}]}~.$](img164.gif) |
(4.2) |
Since the function given by Equation 4.1 does not have an analytic
antiderivative, Romberg numerical integration (see Chapter 4 in
[Press et al. 1996]), was performed.
Cumulative galaxy number counts that were thus obtained are listed in
Table 4.4.



Next: 4.3 Angular Size
Up: 4. Statistical Model of
Previous: 4.1 Morphological Classification
Contents
Mattia Vaccari
2000-12-05
![\includegraphics[width=\textwidth]{./figures/gdnc.eps}](img157.gif)
![\includegraphics[width=\textwidth]{./figures/gdnc.eps}](img157.gif)