


Next: D.2 Bulge Profile
Up: D. Galaxy Surface Brightness
Previous: D. Galaxy Surface Brightness
Contents
The properties of galaxy surface brightness radial profiles can be derived
in a general form using Sersic law, first introduced by
[Sersic 1968] and also known as 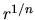 law or generalized
de Vaucouleurs law. This can be written as
law or generalized
de Vaucouleurs law. This can be written as
![$\displaystyle \Sigma(r)=\Sigma_e \,\exp \left( -b_n \left[ \left( \frac{r}{r_e} \right)^{1/n} -1 \right] \right)~.$](img391.gif) |
(D.1) |
where 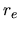 is the effective radius, or the radius within which the galaxy
emits half its brightness,
is the effective radius, or the radius within which the galaxy
emits half its brightness, 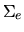 is the surface brightness at
is the surface brightness at 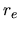 and
and
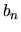 is a positive parameter that, for a given
is a positive parameter that, for a given 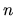 , can be determined from
the definition of
, can be determined from
the definition of 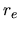 and
and 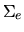 .
The value of
.
The value of 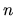 determines the degree of concentration of the profile,
quantified e.g. by the fraction of energy emitted within a given number of
effective radii, the profile being steeper or less concentrated for
higher
determines the degree of concentration of the profile,
quantified e.g. by the fraction of energy emitted within a given number of
effective radii, the profile being steeper or less concentrated for
higher 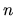 and conversely flatter or less concentrated for lower
and conversely flatter or less concentrated for lower 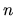 .
Particularly interesting special cases are the bulge-like
.
Particularly interesting special cases are the bulge-like 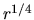 profile
for
profile
for 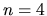 and the disk-like exponential profile for
and the disk-like exponential profile for 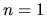 , which will be
discussed in greater detail in Sections D.2 and
D.3.
, which will be
discussed in greater detail in Sections D.2 and
D.3.
According to Equation D.1, the brightness integrated within a
given radius 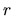 is given by
is given by
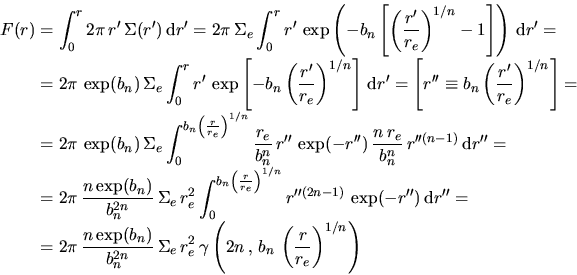 |
(D.2) |
where 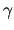 is the incomplete gamma function.
The total brightness predicted by the profile is
is the incomplete gamma function.
The total brightness predicted by the profile is
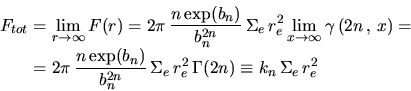 |
(D.3) |
where 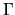 is the gamma function. This relation, remembering that,
by definition of effective radius, it is
is the gamma function. This relation, remembering that,
by definition of effective radius, it is
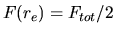 , can be used to
obtain an equation linking
, can be used to
obtain an equation linking 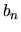 and
and 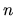 . After cancellation of common terms,
one obtains
. After cancellation of common terms,
one obtains
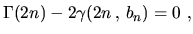 |
(D.4) |
a non-linear equation which can only be solved numerically, e.g. via
the Newton Method (see Section 9.7 in [Press et al. 1996]). Values of 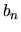 and
and 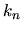 corresponding to integer values of
corresponding to integer values of 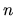 from 1 to 10 are given in
Table D.1.
from 1 to 10 are given in
Table D.1.



Next: D.2 Bulge Profile
Up: D. Galaxy Surface Brightness
Previous: D. Galaxy Surface Brightness
Contents
Mattia Vaccari
2000-12-05
![$\displaystyle \Sigma(r)=\Sigma_e \,\exp \left( -b_n \left[ \left( \frac{r}{r_e} \right)^{1/n} -1 \right] \right)~.$](img391.gif)
![]() is given by
is given by