Signal-to-Noise Ratio Calculation
Under the assumption that an observation (or, equivalently, an
exposure) of an object is made up of a certain number of
frames (in order e.g. to reduce the total number of cosmic
rays affecting the individual readouts and not to fill the potential wells
of the detector' pixels, the conventions used in the following are as
follows:
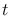 : single-frame exposure time [s]
: single-frame exposure time [s]
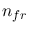 : number of frames composing an oservation [pure number]
: number of frames composing an oservation [pure number]
-
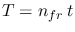 : single-observation exposure time [s]
: single-observation exposure time [s]
- object area : the angular size of the sky region over which a point source is
spread, either due to diffraction effects or to the source being physically
extended on the sky [solid angle - sr]
 : number of pixels within the object area
: number of pixels within the object area
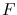 : total electron counts during
: total electron counts during 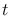 [ e
[ e ]
]
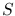 : electron counts from the object during
: electron counts from the object during 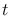 [ e
[ e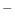 ]
]
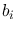 : electron counts from the instrumental background per pixel during
: electron counts from the instrumental background per pixel during 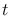 [ e
[ e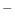 ]
]
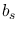 : electron counts from the sky background per pixel during
: electron counts from the sky background per pixel during 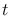 [ e
[ e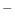 ]
]
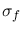 : standard error of generic estimated flux
: standard error of generic estimated flux 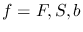 [ e
[ e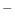 ]
]
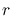 : total readnoise per pixel [ e
: total readnoise per pixel [ e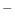 rms]
rms]
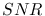 : signal-to-noise ratio in the measurement of the source brightness
during an observation [pure number]
: signal-to-noise ratio in the measurement of the source brightness
during an observation [pure number]
Under these assumptions, 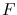 can be written as
can be written as
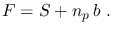 |
(8) |
The physical process of the emission of photons from an astronomical object
can be statistically described in terms of a Poisson distribution.
The standard error in the measurement of 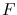 is then due to the intrinsic
Poisson noise associated with
is then due to the intrinsic
Poisson noise associated with 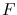 and to the readnoise.
These two contributions sum quadratically yielding for the variance of
and to the readnoise.
These two contributions sum quadratically yielding for the variance of 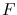
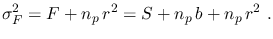 |
(9) |
Since the signal 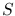 from the object is estimated by subtraction from
from the object is estimated by subtraction from 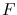 of
the sky background
of
the sky background
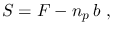 |
(10) |
the variance of 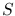 is
is
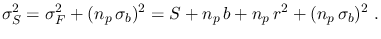 |
(11) |
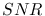 is then
is then
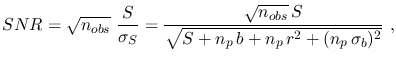 |
(12) |
while
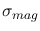 is
is
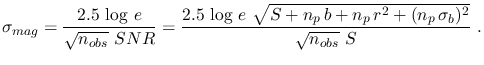 |
(13) |
The overall 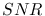 of a number
of a number 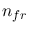 of repeated observations of a given
field is finally given by
of repeated observations of a given
field is finally given by