Optics
The Aperture 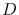 of an optical system is (for radial-symmetry, i.e. circular, telescopes, which we will limit ourselves to consider) the diameter
of its light-collecting area (i.e. its primary mirror or lens).
of an optical system is (for radial-symmetry, i.e. circular, telescopes, which we will limit ourselves to consider) the diameter
of its light-collecting area (i.e. its primary mirror or lens).
The Focal Length 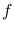 of an optical system is expressed in metres and
defines the image scale on the focal plane, or Focal Scale of the
instrument, meaning that the angular distance
of an optical system is expressed in metres and
defines the image scale on the focal plane, or Focal Scale of the
instrument, meaning that the angular distance
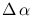 between two
directions on the sky is related to their physical distance
between two
directions on the sky is related to their physical distance 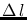 when
they are imaged on the focal plane by
when
they are imaged on the focal plane by
which once "put in numbers" becomes
Similarly, the solid angle
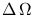 spanned on the sky by a given
sky region is related to the physical area
spanned on the sky by a given
sky region is related to the physical area 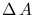 spanned on the focal
plane by
spanned on the focal
plane by
which once "put in numbers" becomes
The Focal Ratio (also referred to as f-number, f-ratio, Aperture Ratio and Relative Aperture and indicated as 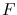 or
or 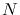 ) is defined as the ratio between the focal length and the aperture, e.g. by
) is defined as the ratio between the focal length and the aperture, e.g. by
It is often useful, and particularly so for simulation purposes, to describe
the entire optical system of an astronomical instrument by means
of a more or less simple mathematical function depending on a few parameters.
In this context, it is also customary to describe the optical response of
most "conventional" telescopes by means of some measure of the "size" of the
instrument's beam.
A functional form often used for these purposes is the ideal diffraction pattern
produced by a circular aperture, or Airy Function, whose exact analytical
expression can be written as
![$\displaystyle AF(\phi) = 4 \left[ \frac{J_1(\phi)-\epsilon\,J_1(\epsilon\,\phi)}{\phi\,(1-\epsilon^2)} \right]^2$](img18.png) |
(1) |
where 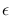 is the telescope obstruction ratio (
is the telescope obstruction ratio (
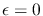 in
ideal systems),
in
ideal systems), 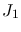 is the Bessel J-function of order 1 and
is the Bessel J-function of order 1 and 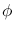 is the dimensionless parameter related to the sky angle
is the dimensionless parameter related to the sky angle 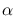 by
by
For an ideal (
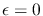 ) system the Airy Function thus reduces to
) system the Airy Function thus reduces to
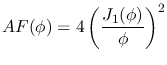 |
(2) |
and its Encircled Energy Function to
![$\displaystyle EEF(\phi) = [ 1 - J_0^2(\phi) - J_1^2(\phi) ]$](img26.png) |
(3) |
The Airy Function and its Encircled Energy Function for an ideal system are tabulated in Table 1 for various values of 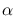 (here expressed in units of
(here expressed in units of 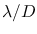 ).
).
As mentioned, in practice a few "fiducial" values are used to characterize
the extension of such an ideal diffraction pattern. An often-used proxy
for an instrument's beam size is the Airy Disk, i.e. the first
zero-brightness circle of the Airy Function. The angular diameter of the
Airy Disk produced by a circular aperture of linear diameter D is
so that the overall size of the "beam", or the solid angle encircled by the Airy Disk, is
Now the "full" Airy Disk above is a rather conservative
(i.e. pessimistic) measure of the "size'"of an instrument's beam,
which is why one often uses the Airy Disk FWHM (or more precisely the
FWHM of the Airy Fucntion) for this purpose instead, whose value is
so that the overall size of the "beam", or the solid angle encircled by
the Airy Disk FWHM, is
The Focal Ratio 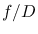 of an optical system is the ratio between its
focal length and aperture, whereas its reciprocal
of an optical system is the ratio between its
focal length and aperture, whereas its reciprocal 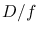 is called
Aperture Ratio.
is called
Aperture Ratio.
For an ideal optical system (100 % reflectivity mirrors), the specific
power 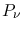 hitting the whole detector when the system is exposed to a
point source of specific brightness
hitting the whole detector when the system is exposed to a
point source of specific brightness 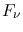 is given by1
is given by1
![$\displaystyle P_{\nu}=\frac{\pi\,D^2}{4}\,F_{\nu}~~~[\mathrm{J \: / \: s \: Hz}]~,$](img40.png) |
(4) |
or equivalently, expressed in photons, by
![% latex2html id marker 1687
$\displaystyle P_{\nu,ph}=\frac{\pi\,D^2}{4\,h}\,\f...
...D^2}{4\,h}\,\frac{F_{\lambda}}{\lambda}
~~~[\mathrm{photons \: / \: s \: Hz}]~.$](img41.png) |
(5) |
Similarly, for an ideal optical system the specific power per unit solid
angle hitting the detector when the system is exposed to a diffuse source of
specific surface brightness
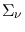 is given by
is given by
![$\displaystyle P_{\nu,sur}=\frac{\pi\,D^2}{4}\,\Sigma_{\nu}~~~[\mathrm{J \: / \: s \: sr \: Hz}]~,$](img43.png) |
(6) |
or equivalently, expressed in photons, by
![% latex2html id marker 1693
$\displaystyle P_{\nu,ph,sur}=\frac{\pi\,D^2}{4\,h}...
...,\frac{\Sigma_{\lambda}}{\lambda}
~~~[\mathrm{photons \: / \: s \: sr \: Hz}]~.$](img44.png) |
(7) |
![$\displaystyle \Delta\,\alpha_{[\mathrm{rad}]}=\frac{\Delta\,l}{f}~,$](img9.png)
![$\displaystyle \frac{\Delta\,l_{[\mathrm{\mu m}]}}
{\Delta\,\alpha_{[\mathrm{arcsec}]}}\simeq4.848\,f_{[\mathrm{m}]}~.$](img10.png)
![$\displaystyle \Delta\,\Omega_{[\mathrm{sterad}]}=\frac{\Delta\,A}{f^2}~,$](img13.png)
![$\displaystyle \frac{\Delta\,A_{[\mathrm{m}^2]}}
{\Delta\,\Omega_{[\mathrm{deg^2}]}}\simeq
3.046\cdot10^{-4}\,f_{[\mathrm{m}]}^2~.$](img14.png)
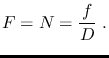
![$\displaystyle \phi=\pi\,\frac{D}{\lambda}\alpha~~~[\textrm{rad}]$](img24.png)
![$\displaystyle \delta_{AD}\simeq2.44~\frac{\lambda}{D}~~~[\mathrm{rad}]~~~~~~\ma...
....503\,\frac{\lambda_{[\mathrm{\mu m}]}}{D_{[\mathrm{m}]}}~~~[\mathrm{arcsec}]~,$](img30.png)
![$\displaystyle \Omega_{AD}\simeq4.68~\left(\frac{\lambda}{D}\right)^2~~~[\mathrm...
...{\lambda_{[\mathrm{\mu m}]}}{D_{[\mathrm{m}]}}\right)^2~~~[\mathrm{arcsec^2}]~.$](img31.png)
![$\displaystyle \delta_{AD,FWHM}\simeq1.02~\frac{\lambda}{D}~~~[\mathrm{rad}]~~~~...
....210\,\frac{\lambda_{[\mathrm{\mu m}]}}{D_{[\mathrm{m}]}}~~~[\mathrm{arcsec}]~,$](img32.png)
![$\displaystyle \Omega_{AD,FWHM}\simeq0.817~\left(\frac{\lambda}{D}\right)^2~~~[\...
...{\lambda_{[\mathrm{\mu m}]}}{D_{[\mathrm{m}]}}\right)^2~~~[\mathrm{arcsec^2}]~.$](img33.png)