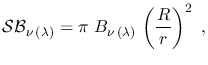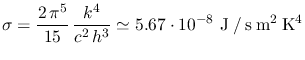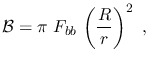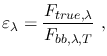Energy, Photons, Blackbodies etc.
The energy of a photon of frequency 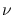 is given by
is given by
where
is Planck's constant and
is the speed of light in a vacuum.
In spectroscopy, the energy of a photon is often expressed by the inverse of its wavelength, or Wave Number
which is generally expressed in
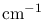 . When using an actual energy
unit is appropriate, one generally uses the electronvolt
. When using an actual energy
unit is appropriate, one generally uses the electronvolt
i.e. the amount of energy equivalent to that gained by a single unbound electron when it is accelerated through an electrostatic potential difference of one volt (in a vacuum). In other words, an electronvolt is equal to one volt (1 volt = 1 joule per coulomb) multiplied by the (unsigned) charge of a single electron. The energy of a photon is related to its wavelength by the following
Planck's law describing the radiation from a blackbody says that the
frequency specific surface brightness, i.e. the energy emitted per unit
time, unit area (of the emitter's surface), unit solid angle and unit frequency
interval, of a blackbody at a temperature 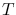 is
is
whereas the corresponding wavelength specific surface brightness, i.e. the
energy emitted per unit time, unit area (of the emitter's surface), unit
solid angle and unit wavelength interval (which is related to the previous
quantity by Equation 25) is
where
is Boltzmann's constant.
The corresponding specific brightness at the receiver, i.e. the energy
received per unit time, per unit area (of the receiver's surface) per unit
frequency/wavelength interval from the whole blackbody (assuming this has a
spherical shape) is instead
where 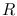 is the radius of the blackbody,
is the radius of the blackbody, 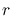 the distance between the
blackbody and the observer, and the
the distance between the
blackbody and the observer, and the 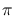 factor arises from integration.
factor arises from integration.
Integration of one of the aforementioned formulae yields the energy emitted
per unit time per unit area (of the emitter's surface) at all
frequencies/wavelengths. This turns out to depend on the temperature of the
blackbody only, a result also known as Stefan-Boltzmann's law
where
is Stefan-Boltzmann's constant.
The corresponding brightness at the receiver, i.e. the energy received
per unit time, per unit area (of the receiver's surface) at all frequencies/wavelengths
from the whole blackbody (assuming this has a spherical shape) is instead
where 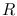 is the radius of the blackbody,
is the radius of the blackbody, 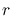 the distance between the
blackbody and the observer, and the
the distance between the
blackbody and the observer, and the 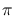 factor arises from integration.
factor arises from integration.
Similarly, the derivation of the expression given for
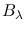 yields
the relation between the wavelength of its maximum and the temperature,
or Wien's displacement law
yields
the relation between the wavelength of its maximum and the temperature,
or Wien's displacement law
The Emissivity
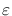 of a body is defined as the ratio
of a body is defined as the ratio
between its wavelength specific brightness and the wavelength specific
brightness of a blackbody at the same temperature 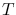 .
The Absorptivity of a body is similarly defined as the ratio of
the energy absorbed by a body and by a blackbody at the same temperature.
Kirchoff's law states that at thermal equilibrium, the emissivity of a body
equals its absorptivity. In general, the emissivity of a body is wavelength-dependent,
but by definition a blackbody has got
.
The Absorptivity of a body is similarly defined as the ratio of
the energy absorbed by a body and by a blackbody at the same temperature.
Kirchoff's law states that at thermal equilibrium, the emissivity of a body
equals its absorptivity. In general, the emissivity of a body is wavelength-dependent,
but by definition a blackbody has got
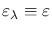 .
By extension, a graybody is a body for which
.
By extension, a graybody is a body for which
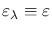 , and
thus
, and
thus
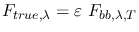 .
.
In order to describe dust emission astronomers often use a modified graybody
where 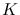 is a constant, and
is a constant, and 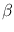 (whose value is between 1 and 2) is called the dust emissivity index. For such a modified graybody, in other words,
(whose value is between 1 and 2) is called the dust emissivity index. For such a modified graybody, in other words,
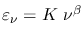 .
.
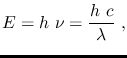
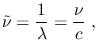
![$\displaystyle E_{[\mathrm{eV}]}=\frac{1.24}{\lambda_{ [ \mu \mathrm{m}]}}~.$](img52.png)
![$\displaystyle B_\nu(\nu,T)=\frac{2\,h\,\nu^3}{c^2}\left[\exp\left(\frac{h\nu}{kT}\right)-1\right]^{-1}~~~[\mathrm{J \: / \: s \: m^2 \: sr \: Hz}]~,$](img54.png)
![$\displaystyle B_\lambda(\lambda,T)=\frac{\nu^2}{c}\,B_\nu(\nu,T)=
\frac{2\,h\,c...
...}{\lambda kT}\right)-1\right]^{-1}~~~[\mathrm{J \: / \: s \: m^2 \: sr \: m}]~,$](img55.png)